
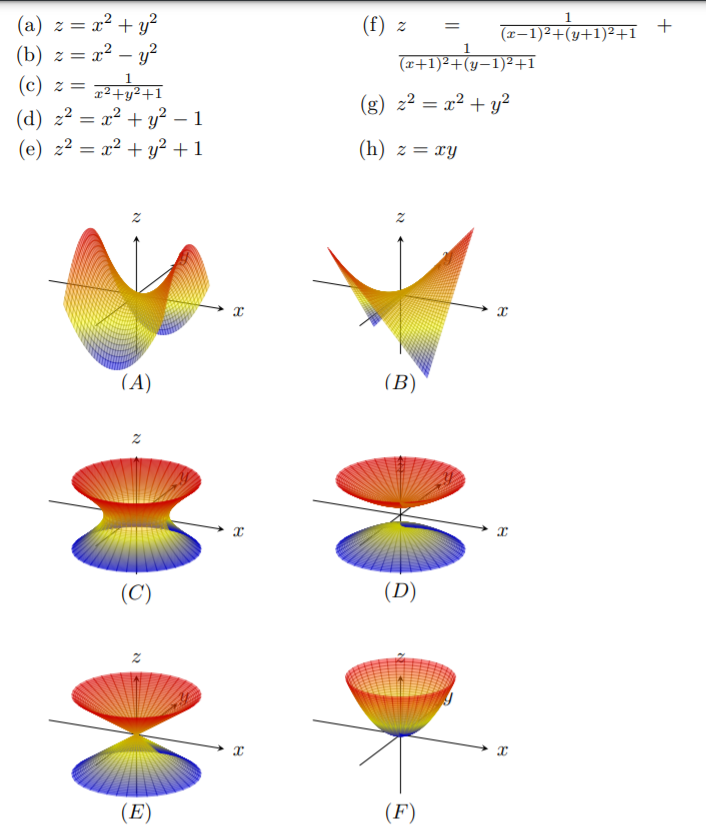
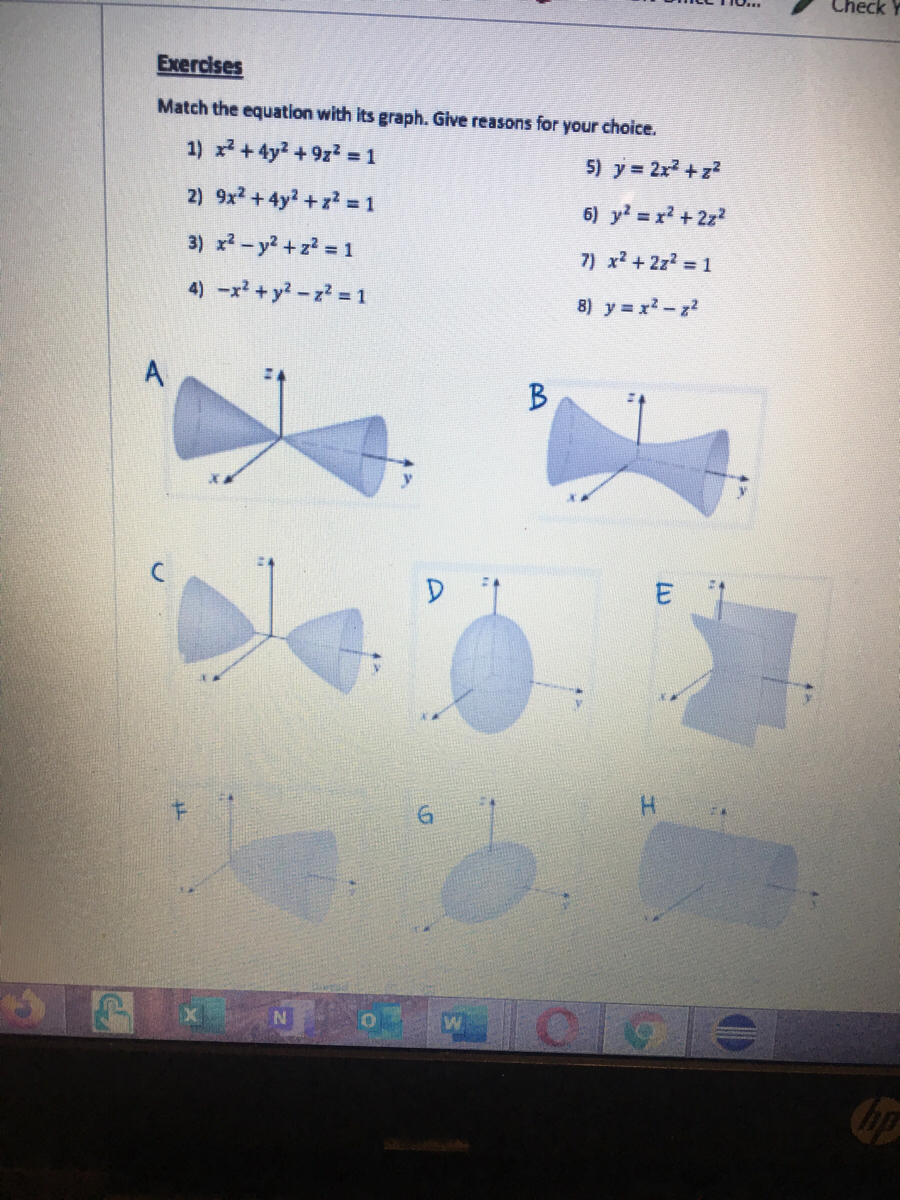
How Do You Find The Volume Of A Solid Where X 2 Y 2 Z 2 9 Is Bounded In Between The Two Planes Z 2x 2 And Z 2x 3 Socratic
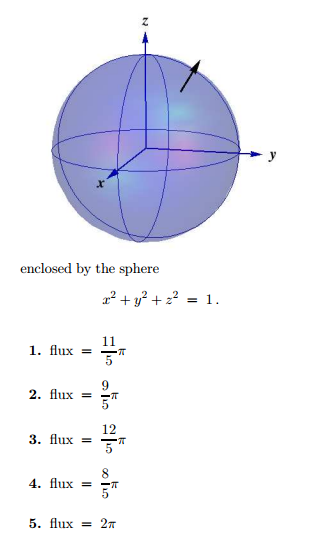
The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6 Since y^2 = x − 2 is a relation (has more than 1 yvalue for each xvalue) and not a function (which has a maximum of 1 yvalue for each xvalue), we need to split it into 2 separate functions and graph them together So the first one will be y
X^2+y^2+z^2=16
X^2+y^2+z^2=16-The value of x y z if x^2 y^2 z^2 = 18 and xy yz zx = 9 is Solve Study Textbooks GuidesWolframAlpha Computational Intelligence Natural Language Math Input NEW Use textbook math notation to enter your math Try it × Extended Keyboard Examples Compute expertlevel answers using Wolfram's breakthrough algorithms, knowledgebase and AI technology
2
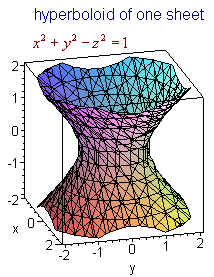
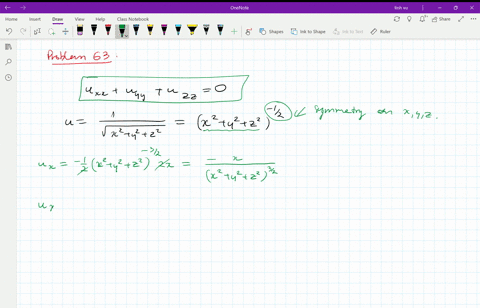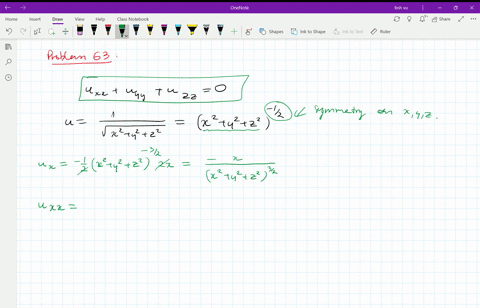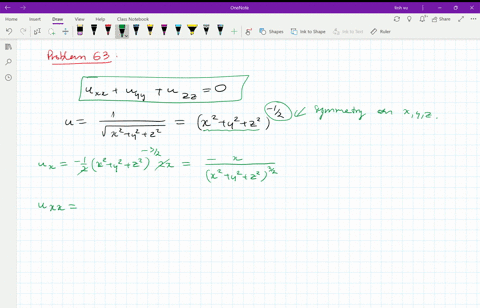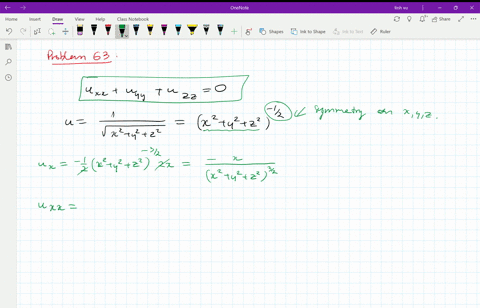
See the answer See the answer See the answer done loadingZ 2 q 1−x2−y 2 9 0 f(x,y,z)dzdydx Treating S as a x simple region, we have for fixed y − z, x going from 0 to q 1− y2 9 − z2 4 The projected region in the y−z plane can be described as a zsimple region in the y − z plane and described by ((y,z) 0 ≤ z ≤ 2 r 1− y2 9,0 ≤ y ≤ 3) So, the above integral is the same as Z 3Answer (1 of 5) It's the equation of sphere The general equation of sphere looks like (xx_0)^2(yy_0)^2(zz_0)^2=a^2 Where (x_0,y_0,z_0) is the centre of the circle and a is the radious of the circle It's graph looks like Credits This 3D
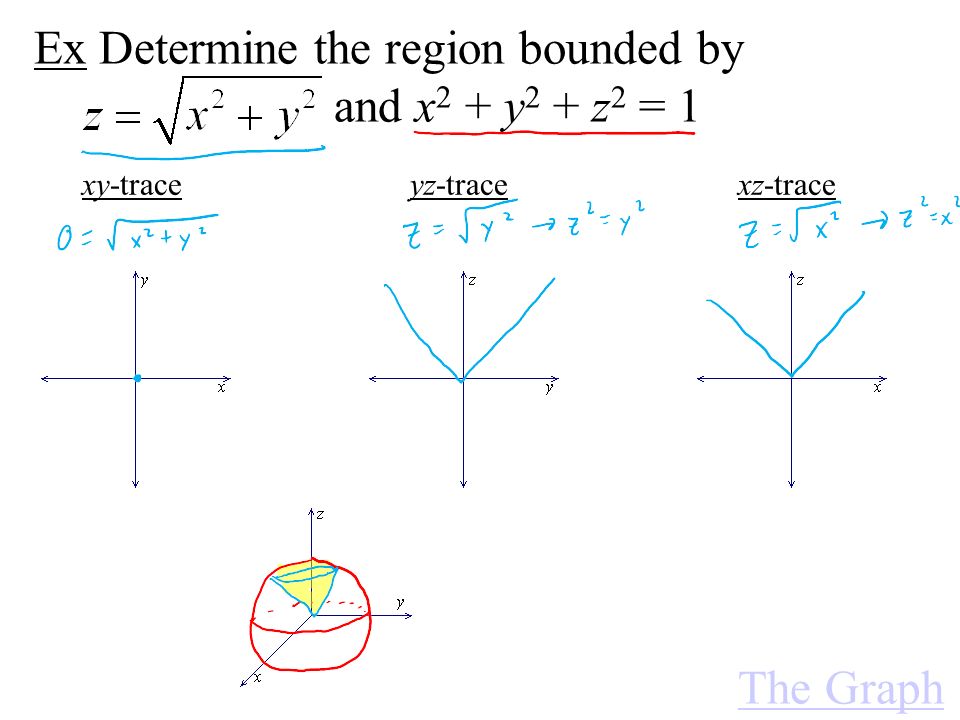
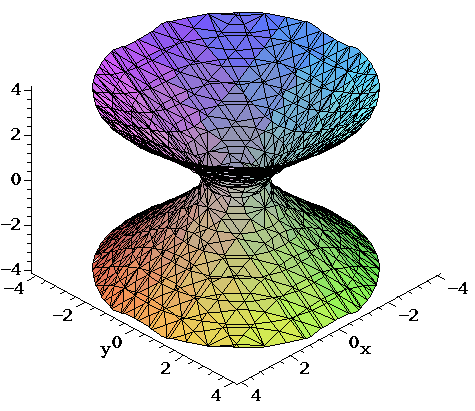
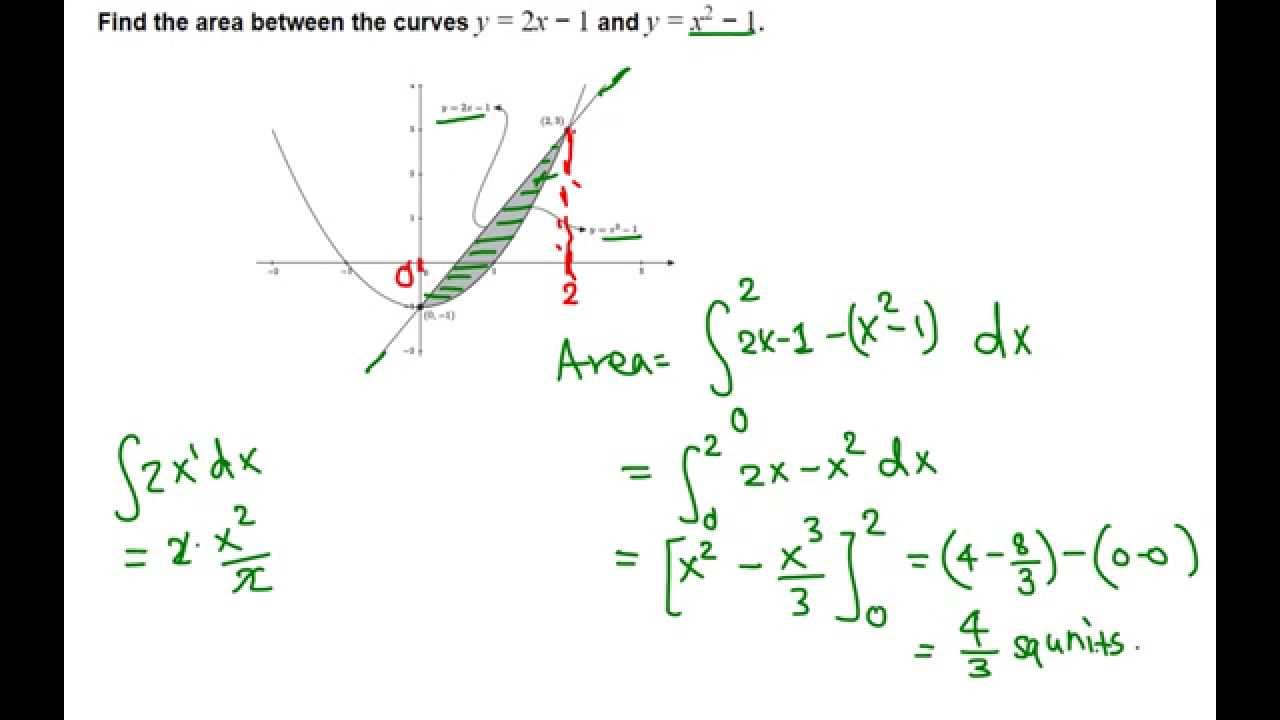
The left curve is the sideways parabola x = y2 The right curve is the straight line y = x − 2 or x = y 2 The limits of integration come from the points of intersection we've already calculated In this case we'll be adding the areas of rectangles going from the bottom to the top (rather than left to right), so from y = −1 to y = 2The paraboloid y = x z is shown in blue and orange The paraboloid x = y z is shown in cyan and purple In the image the paraboloids are seen to intersect along the z = 0 axis If the paraboloids are extended, they should also be seen to intersect along the lines z = 1, y = x;Y^2 = x^2 z^2 has the form of an equation for a circle So, you are stacking, in the y direction, circles of increasing radius, one on top of the other Share answered at 2114 Tomek Dobrzynski 69 3 Add a comment Your Answer Post Your Answer
X^2+y^2+z^2=16のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 | ||
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
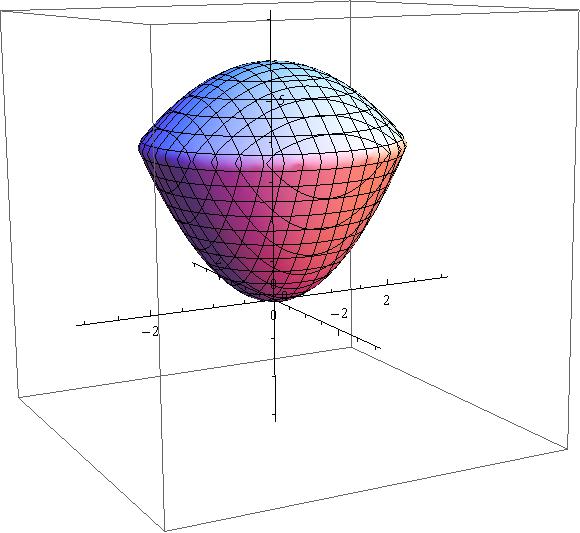 |  |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
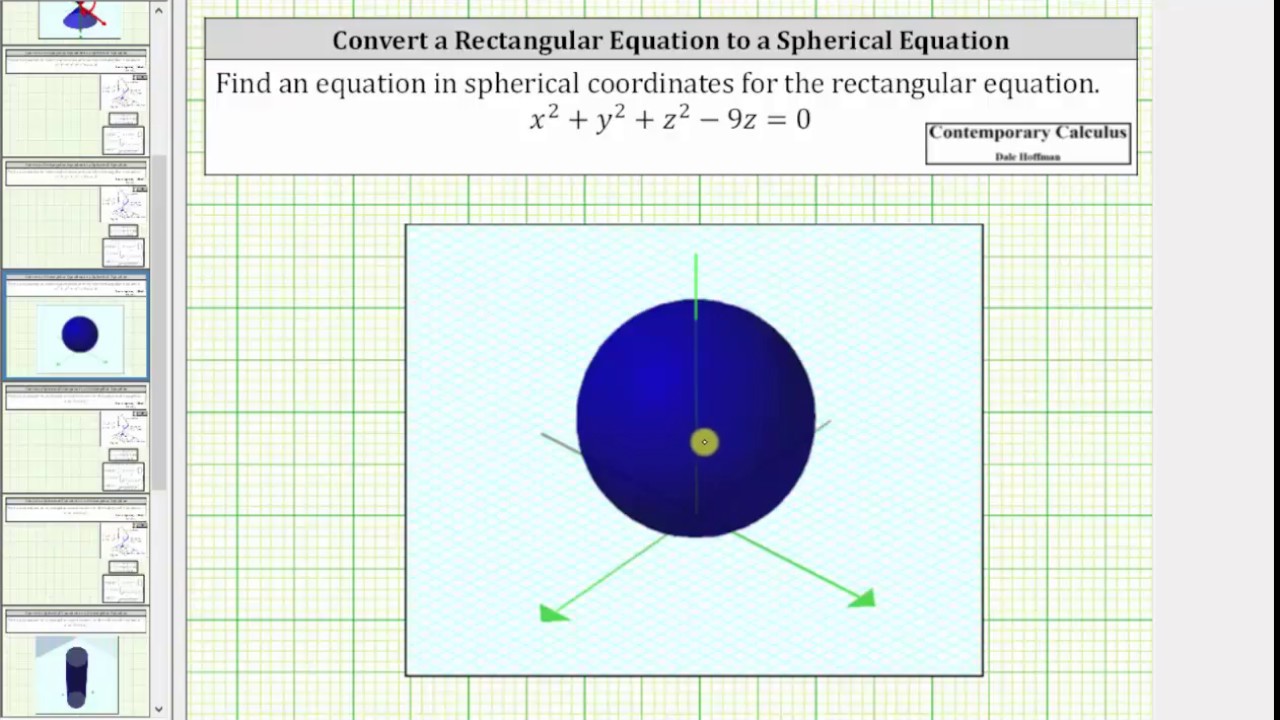 | 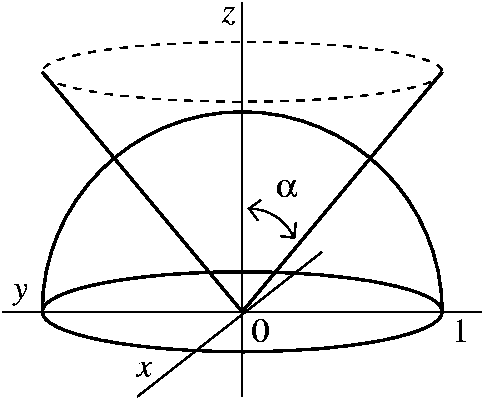 | |
 |  |  |
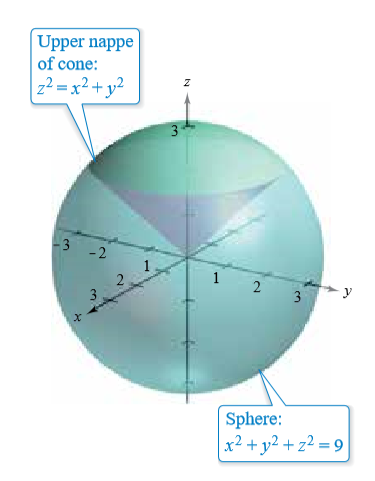 |  | |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 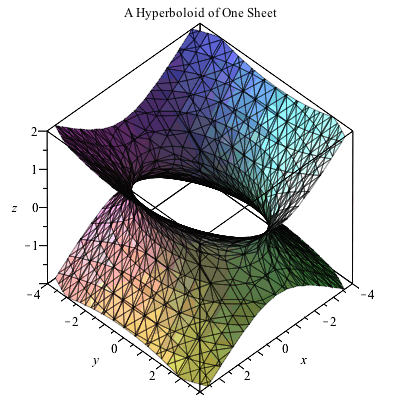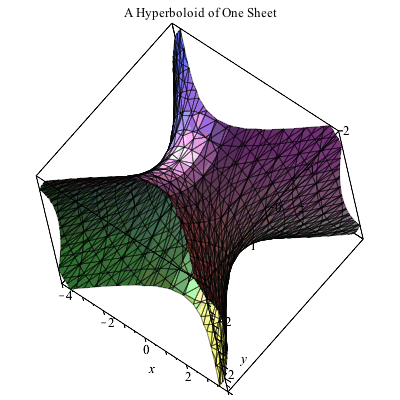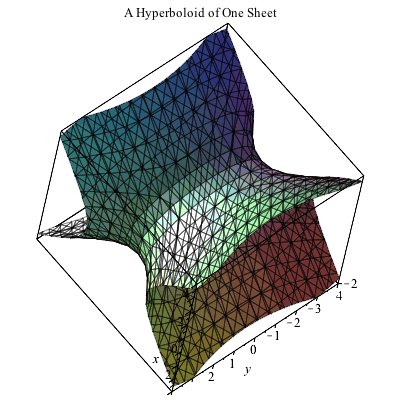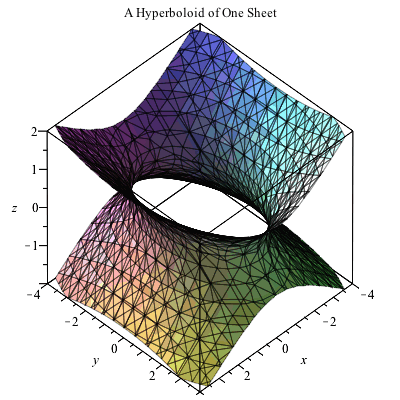 |
 | 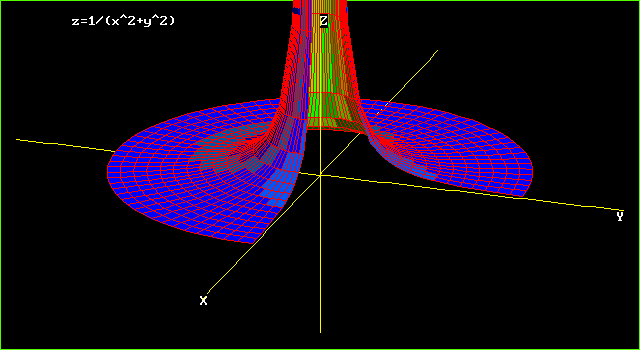 |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 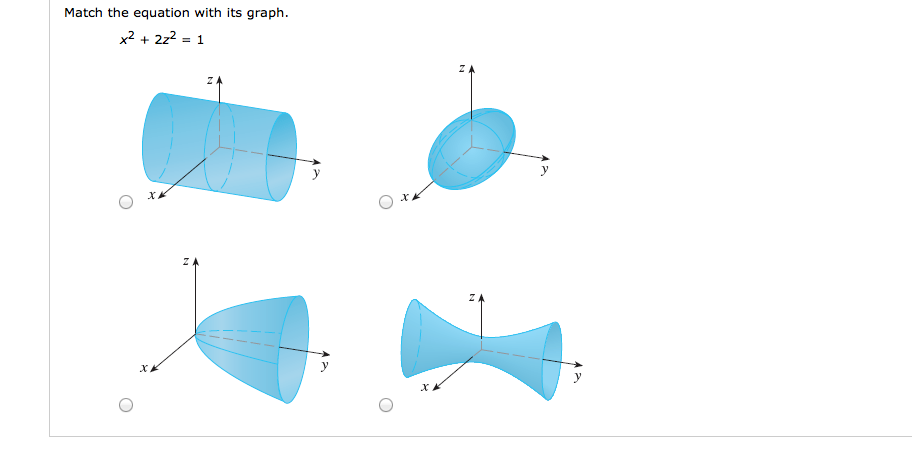 |  |
 |  |  |
 |  | |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
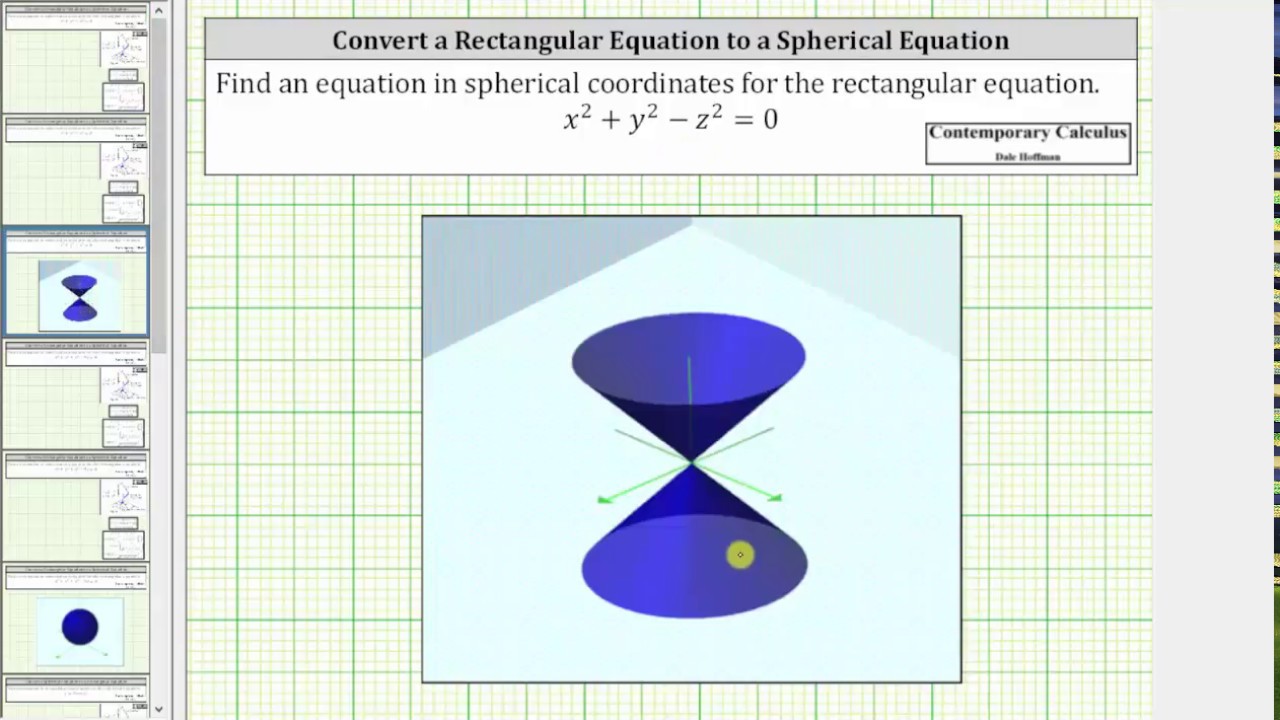 |  | |
 |  | |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
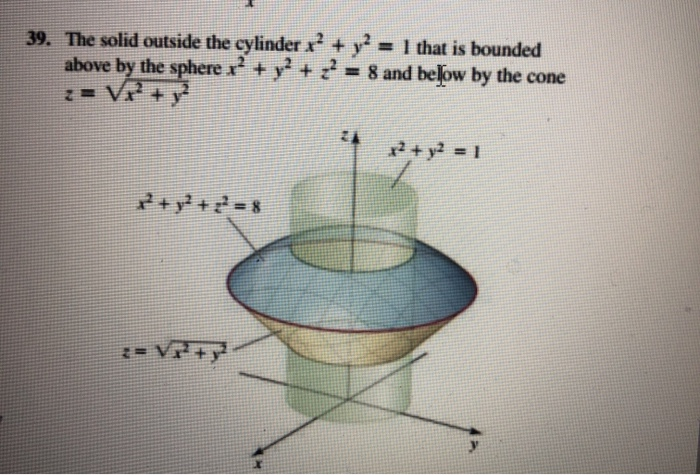
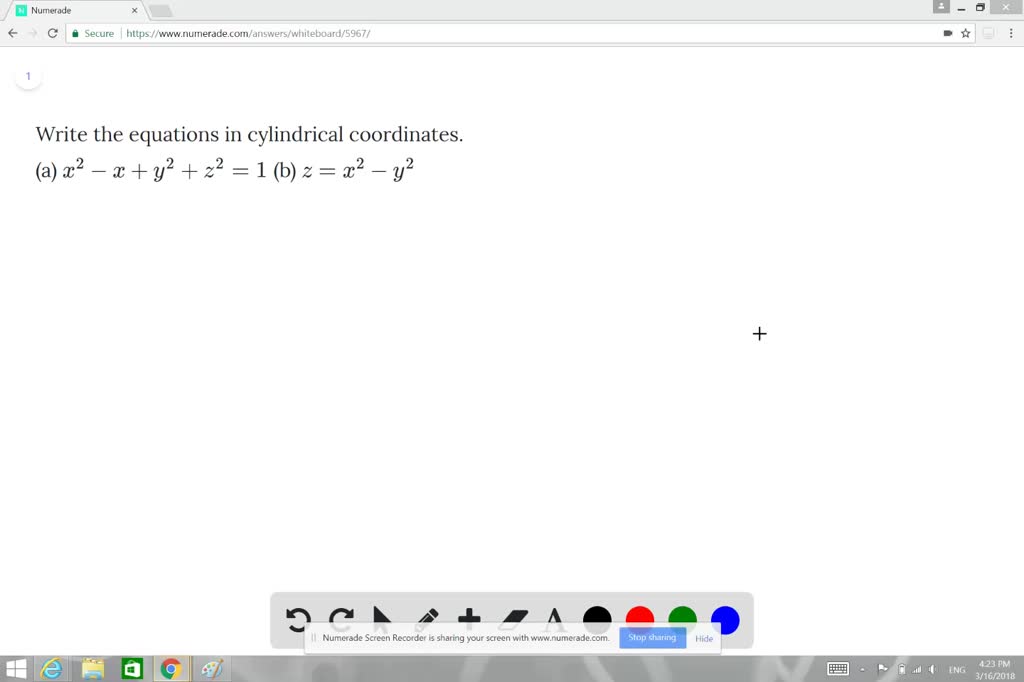 |  |  |
 |  |  |
 |  |  |
「X^2+y^2+z^2=16」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
Solution for x^2y^2z^2=1 equation Simplifying x 2 y 2 z 2 = 1 Solving x 2 y 2 z 2 = 1 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add '1y 2 ' to each side of the equation x 2 y 2 1y 2 z 2 = 1 1y 2 Combine like terms y 2 1y 2 = 0 x 2 0 z 2 = 1 1y 2 x 2 z 2 = 1 1y 2 Add '1z 2 ' to each side of theGet the answers you need, now!
Incoming Term: x^2+y^2+z^2=1, x^2+y^2+z^2 =1/3, x^2+y^2+z^2=1 graph, x^2+y^2+z^2=1 in spherical coordinates, x^2+y^2+z^2=16, x^2+y^2+z^2=1 parametrization, x^2+y^2+z^2=16 graph, x^2+y^2+z^2=1 in cylindrical coordinates, x^2+y^2+z^2=16 in spherical coordinates, x^2+y^2+z^2=1 xy+yz+zx,




0 件のコメント:
コメントを投稿